One of the main reason that many models can’t get them predicted results is overfitting. Overfitting occurs when a model captures idiosyncrasies of the input data, rather than generalizing. In another words, it means that the model focuses more on specific details rather than the whole trend, like green model in picture 1:
picture 1 : https://en.wikipedia.org/wiki/Overfitting
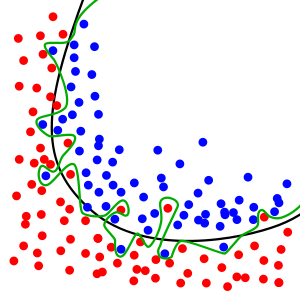
The methods of avoiding or reduce this overfitting situation are :
- Provide more sample data
- Hyper-Parameter tuning
- Take a Bayesian approach
- Model Regularization
I talk about regularized this time. Since least squares regression methods, where the residual sum of squares is minimized, can be unstable, particularly in collinearity models, which is the model with a linear association between two explanatory variables. Regularization adds penalties to more complex models and then sorts potential models from least overfit to greatest; The model with the lowest “overfitting” score is usually the best choice for predictive power.
About Penalty :
L1&L2 Regularization :
picture 2 : https://towardsdatascience.com/
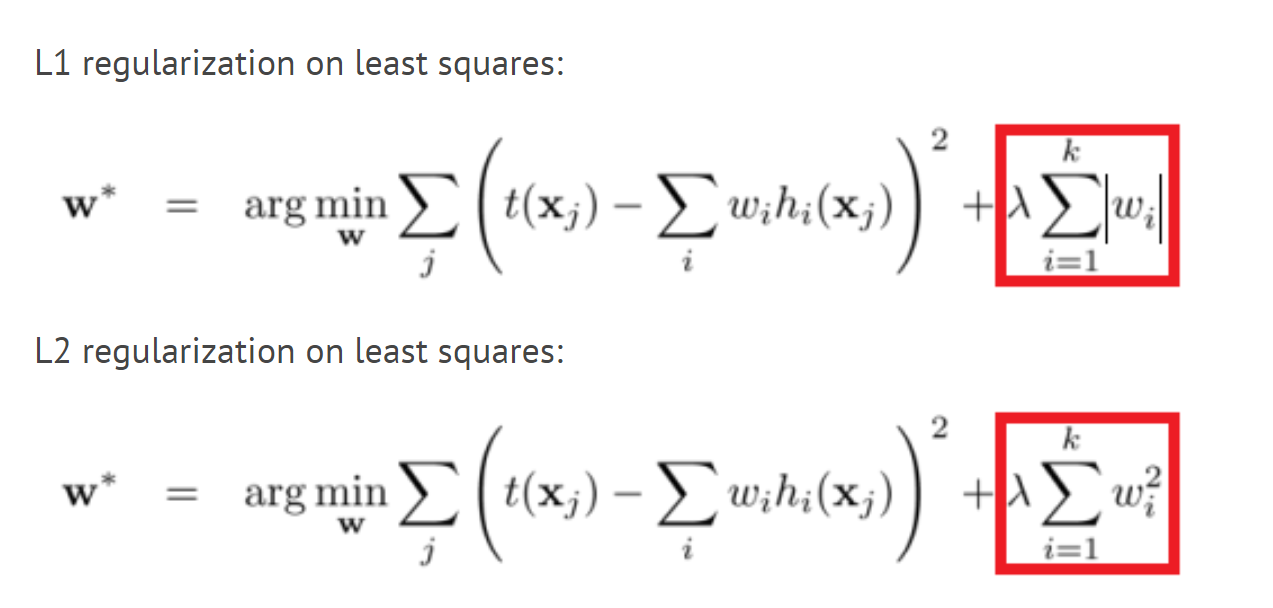
From the functions I find that the different is the last part, which is that, for L1-regularization, is tangent by a line while for L2-regularization, is tangent by a circle, like picture 3 :
picture 3 : https://codeburst.io/what-is-regularization-in-machine-learning-aed5a1c36590
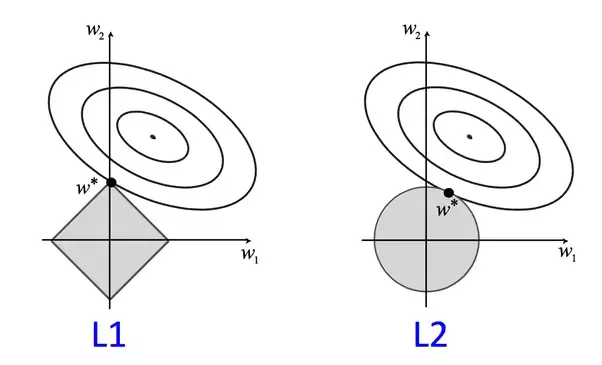
L1 regularization adds an L1 penalty equal to the absolute value of the magnitude of coefficients. In other words, it limits the size of the coefficients. while L2 regularization adds an L2 penalty equal to the square of the magnitude of coefficients. And elastic nets combine L1 & L2 methods, like picture 4 :
picture 4 : http://www.ds100.org/sp17/assets/notebooks/linear_regression/Regularization.html
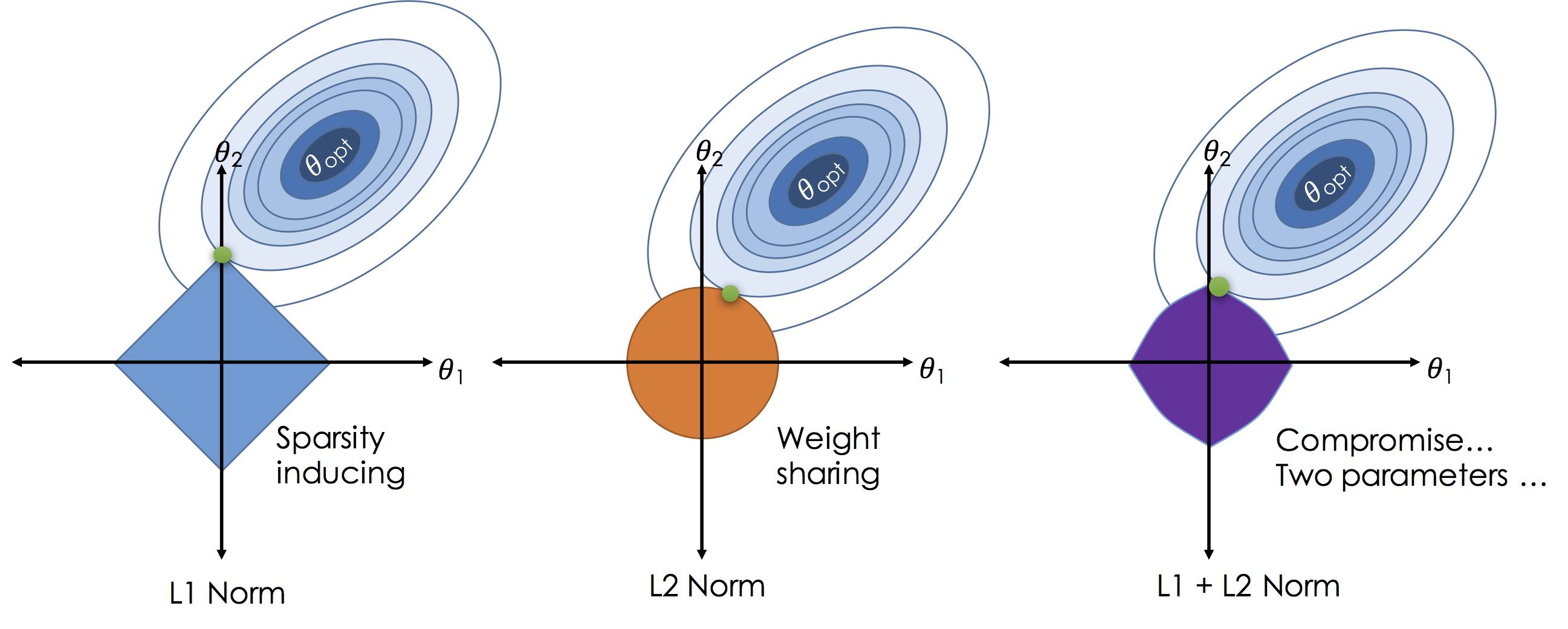
All of SVM algorithms are L2-regularization and can be controlled by parameter penalty in python code :
linear_model.SGDRegressor(loss='squared_loss', penalty=None, random_state=13)
linear_model.SGDRegressor(loss='squared_loss', penalty='l2', random_state=13)
For the models with many variables, penalty with ‘l2’ is a good way to avoid overfitting.